Algebraic effects are a functional approach to manage side effects

The world outside our computers is unpredictable and interacting with it can make programs unreliable. However, programs must interact with the wider world to do anything useful.

This unpredictability manifests in many places. I’ve dealt with an incident caused by an application losing write permissions to the file system. Write access wasn’t thought to be necessary but it turned out a library we used was writing to temporary files for a cache. Removing the ability to write the cache crashed the program.

We work to bring predictability to our programs by controlling access to the world. For example, writing reliable tests requires the use of mock services and dummy databases.

Much development time is spent managing and understanding the side effects - algebraic effects offer a consistent and ergonomic approach. This single abstraction supersedes exception handling, state, iterators async-await and more by generalising the communication between a program and the world.

EYG is a language with the goal of making software development more predictable. Algebraic effects are a key feature of the language. This post aims to explain the concept of effects. The explanation applies to any language that has, or might add in the future, effects.

To explain effects we start with the basics and look at the functions that make up our programs.

This post is part of a talk I gave, the section on algebraic effects starts at 14:17

What is a function?

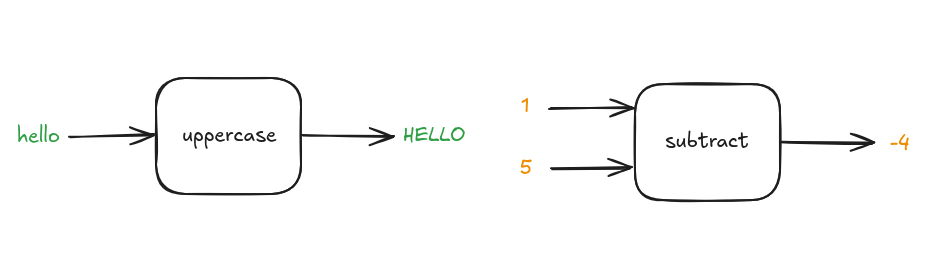
Precisely defined in mathematics “a function is the relation between an input and an output, so that every input has exactly one output”. uppercase is a simple function where input and output are a single string. subtract is a function with two integers as input and a single integer output.

Diagrams for these simple functions look like this.

Here is an EYG program that uppercases the string value "hello". The @std:2 term references a package release. The package name is std and we are depending on the second version of the package.

All snippets in this post can be edited and run. Click on the code to get started.

See the documentation for more details about the EYG language and editor.

Using functions

New functions can be defined by composing other functions and values.

For example my_function takes a single input from which it subtracts 5 before calculating the absolute value.

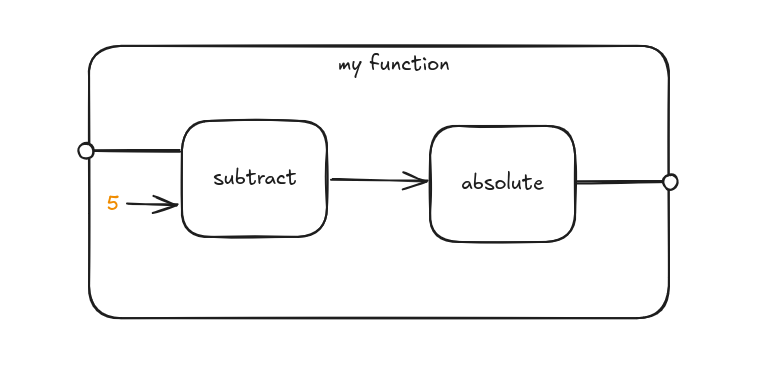
Circles indicate there is a value that is not yet provided.

Functions are themselves values and can be the input, or output, of other functions. Describing a language as having “first class functions” means that the language allows functions to put input or output of other functions.

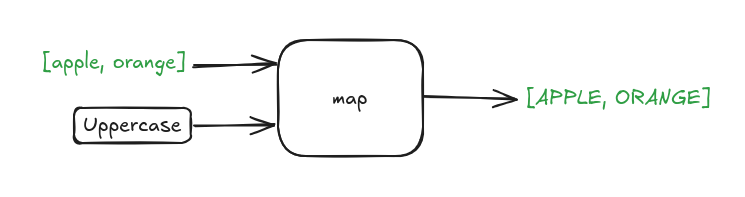
In this example the map function takes two values. The first input is a list of items and the second is the function uppercase. Every item in the list is mapped to a new value using the uppercase function.

Side effects and side causes

These next operations look sensible and indeed familiar when considering other languages. However, these operations are not functions. Why? Because a function is only a fixed relation from input to output. The same input must always produce the same output.

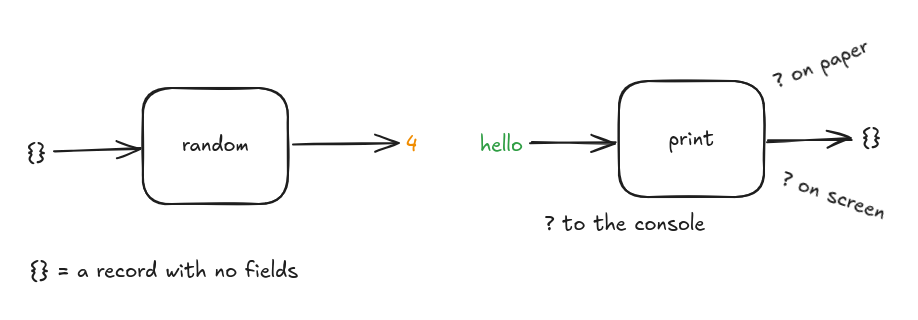
A print function can be implemented that takes a string and returns an empty record, but without the outside world it will only be able to discard the input message.

The random function always takes the same input so must always produce the same output. It’s possible to have a random function that always returns 4. That is probably not the behaviour expected for a function called random.

xkcd

I use the term operation to distinguish from functions. Often the term pure function is used for a mathematical function and impure function for all the rest.

Most languages have implicit effects. Calling the operation random or print makes calls to the outside world adhoc without it being visible to the program. The language will have decided ahead of time all the side effects that a program might use.

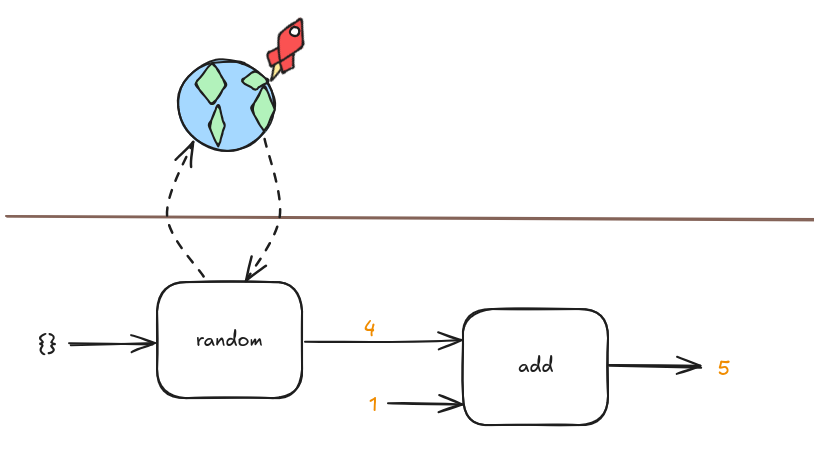
Side effects expose the program to the whole world. Nothing in the program actually knows the limits of what the side effects do. The whole world is big, complex and includes effects that might be permanent like launching the missiles.

Controlling side effects

Because the external world is large and messy it is good practice to isolate our program, as much as possible, from the world. Many languages control communication to the outside world to ensure predictable behavior.

xkcd

Haskell uses the IO monad to manage effects. Working with monads is a whole thing that we will not get into here.

Other languages make use of dependency injection to control effects. For example an API client might be a required argument to a business function so that different implementations can be provided in staging or production.

Architectural patterns like functional core, imperative shell or hexagonal architecture exist to organise communication to the outside world.

In tests, effects are controlled using mocks, stubs or doubles.

Algebraic effects are another way to manage side-effects and side-causes. They require no syntactic overhead or force a particular architecture.

But first, a quick aside into continuations.

Continuations

Explaining continuations is easiest with a concrete example.

Dashed lines indicate that although negate is an argument to add_k it is helpful to consider a value flowing in the opposite direction.

In the first diagram add is function in the direct style. The direct style means no continuations, add returns the sum of the two values and the surrounding program passes the result to negate.

Compare add with add_k which accepts an additional third argument k. This k is the continuation. add_k is responsible for calling the continuation with the sum of the other two values. And the return value of add_k is the return of the whole program.

A continuation is essentially the same as a callback.

You may have heard of callback hell a situation where working with many callbacks becomes painful. Algebraic effects don’t suffer from “callback hell” because the continuation is passed automatically.

Algebraic effects

Algebraic effects consistently model a program’s interaction with the outside world. Programs can handle all side-effects, side-causes using them, this includes:

• Input and output operations
• Non determinism i.e. random
• Time
• Exceptions
• Concurrency
• Mutability

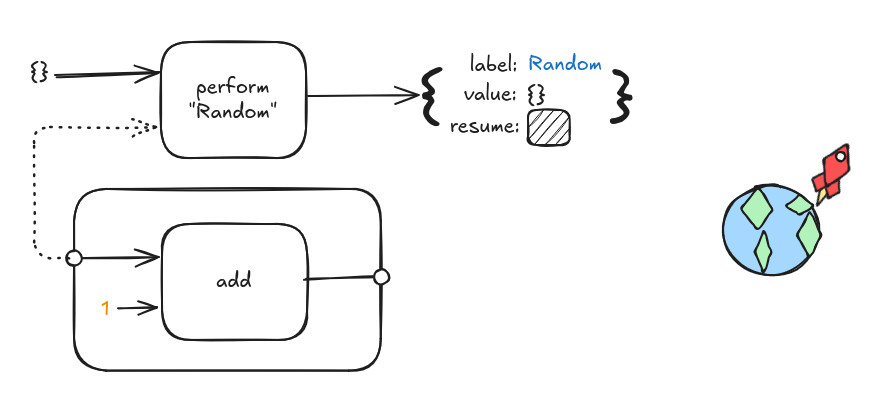
To use an effect the program uses the perform keyword. This halts the program and creates an effect. The effect consists of three fields.

1. A label indicating what kind of effect it is.
2. A value which is any data from the program to the external world.
3. A resume function which is the continuation representing the rest of the program.

Instead of a program calling a random “function” with implicit side effects it will perform the Random effect.

The program is now pure as it consists of inputs and outputs without a reliance on the outside world. However, instead of returning the result we want our program returns a request to the outside world, the effect. In English the effect is saying - please call resume when you have a value that satisfies the “Random” effect.

Once the surrounding environment has an answer for that effect it can call resume to continue the program. The resume function is also pure. To perform more effects another effect will be returned for the world to act on, in it’s own time.

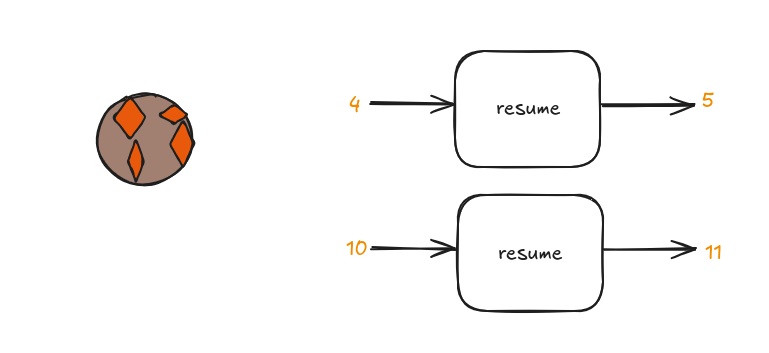
Because resume is just a function it can be called more than once and potentially at a much later time.

Algebraic effects automatically pass the continuation when an effect occurs. So you write regular code like below.

Type inference

Algebraic effects can infer all the requirements a function has on the outside world. To answer “does this function call the network?” or “does this function need a file system” referring to the function type signature will provide the answer.

Using algebraic effects is more precise than using IOMonad. With IOMonad a function can only be pure or impure, there is no differentiation between random or accessing the network.

Effects compose cleanly.

The function f has only the Now effect in it’s type signature and g only the Alert effect. The function h has a type signature that includes both effects.

Conclusion

Algebraic effects are a convenient abstraction for modelling the interaction between a program and the world. Programs are only a set of instructions. It is the job of a computer to run those instructions.

There are several benefits to algebraic effects.

• They allow the effects of any function to be precisely inferred.
• They are cleaner when compared to other approaches for controlling effects.

In a later post we will discuss handlers and how to intercept and modify effects in our programs. For now the best description I have of effect handlers is the EYG documentation